第2章 群体药代动力学基本原理

第一节 基本原理

群体药动学药效学是一门将统计学模型应用于药理学领域的学科，其目的是用数学表达式定量表征药物在机体的吸收和处置过程、机体对药物的反应过程和疾病进展等，旨在根据患者的特征信息预测药物浓度和疗效，制定和调整给药方案。
个体模型描述个体的数据。群体模型在个体模型的基础上，增加了解释个体间参数变异的大小及来源的模型。混合效应模型是一种同时考察固定效应和随机效应的模型，以及模型参数的分布、集中趋势和离散程度等，以下将作详细介绍。

一、个体模型和群体模型

（一）个体模型

个体模型是表征个体数据特征的模型，可由一个结构模型和一个统计学模型组成。结构模型即经典的药动学药效学模型。统计学模型即表征模型预测值与个体观测值差异的模型。后文将模型预测值简称为预测值，个体观测值简称为观测值。构建个体模型可将观测值与预测值相联系，描述观测值和预测值的差异情况。

1. 结构模型：经典的药动学-药效学模型
2. 统计学模型：表征模型预测值与个体值差异的模型

口服一级吸收和一级消除的一房室模型：

```mermaid
graph LR
Dose*F-->A
A( 药物储存室) --> C(中央室)
C --> 消除
```
[](http://139.224.52.201/wp-content/uploads/2023/03/Snipaste_2023-03-11_21-25-19.png)

单次给药后血药浓度随时间变化可表示为：
$$
Cpred,i= ka * F * Dose / V* （ka-ke） * （ e ^ {-keti}- e ^ {-kati}）
$$

其中,ka是一级吸收速率常数,ke是一级消除速率常数,Dose是给药剂量,F是吸收分数,即进入体循环的药量占给药剂量的百分数,V是分布容积,Cpred牞 i 是单次给药后第i 个时间点的预测值｡

（二）群体模型

群体模型是在个体模型基础上,增加了个体间变异的模型｡个体间变异模型描述了个体参数的变异大小以及变异的来源｡群体模型不仅包含了个体模型的所有组分,还包含了个体间变异相关的参数和表征群体特征的子模型,用以描述群体的典型值和变异程度｡
群体模型包含了多层嵌套的随机效应｡第一层是参数水平,描述了个体模型参数的变异;第二层是个体观测值水平,描述了个体预测值的变异｡第二层嵌套在第一层之上,即在不同的参数水平下产生的预测值｡随机效应的嵌套性,也是群体模型与个体模型之间的差异所在｡

在个体模型基础上增加个体间变异
多层嵌套：
第一层：参数水平
第二层：个体观测值水平
第二层嵌套在第一层之上

二、非线性混合效应模型

（一）结构模型

药动学结构模型通常包括了吸收模型和处置模型｡常见的吸收模型包括简单的零级吸收模型､一级吸收模型,以及复杂的渐进吸收模型､混合吸收模型､威布尔吸收模型等｡一般可选择简单的模型来描述药物的吸收过程｡但对于需要准确估算药物的达峰时间和峰浓度,或描述不同时间段的吸收过程､吸收滞后等特殊的吸收过程,可采用上述复杂的吸收模型｡
药物的处置模型常用房室模型表征,包括一房室､二房室､三房室等｡房室数越多,药动学参数也越多,拟合的药动学过程更准确｡但是房室数越多,模型也越复杂,易导致参数计算的失败｡
在药效学研究中,常用模型包括直接效应模型､效应室模型､翻转模型等｡药动学药效学模型建模过程中可以一步同时拟合药动学和药效学参数,也可先建立药动学模型计算药动学参数,再进一步链接药效学模型计算药效学参数｡

包括吸收模型和处置模型
吸收模型： 简单的零级吸收模型，一级吸收模型；复杂的渐进吸收模型，混合吸收模型，威布尔吸收模型。
处置模型： 常用房室模型表征，一室模型，二室模型，三室模型。
药效模型： 直接效应模型，效应室模型，翻转模型。

（二）固定效应

固定效应一般用THETA表示，数值下标表示不同的固定效应
固定效应定义群体的典型值，如：清除率，分布容积，吸收速率，生物利用度等。还包括了协变量，如年龄，体重，性别等

（三）随机效应

随机效应是一类未知的､难以测量或不可观测的因素,用来量化固定效应参数无法解释的变异或模型预测误差｡
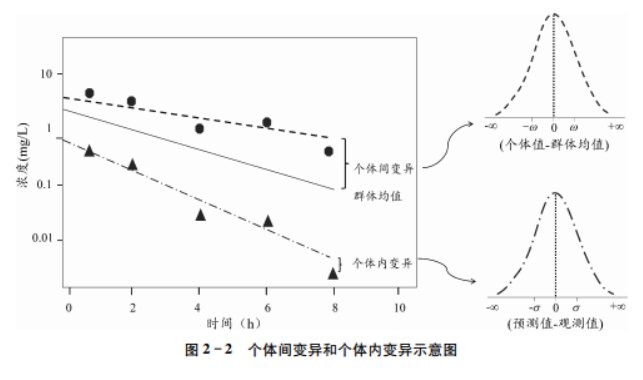
随机效应主要可分为个体间变异(betweensubject variability,BSV)和个体内变异(withinsubject variability,WSV),后者也称为残差变异(residual variability,RUV)｡个体间变异是指个体参数值相对于群体典型值的偏离;个体内变异指个体预测值相对于实际观测值的偏离,两者的含义如图2 2所示｡个体间变异和个体内变异分别用η(ETA)和ε(EPS)表示,一般假设个体间变异和个体内变异均符合正态分布｡

随机效应主要可分为个体间变异和个体内变异

1.个体间变异

(1)定义:个体间变异即个体参数值相对于群体典型值的偏离｡当个体间变异较小时,受试者间的药动学行为相似,各受试者间达到目标浓度所需的剂量接近,可使用固定剂量｡当个体间变异较大时,统一的固定剂量则不能满足所有用药人群的需求｡此时,若已知变异的来源,则可据此调整剂量｡

个体间变异：个体参数相对于群体典型值的偏离，用ETA(η)表示
(2)常用函数表达式:加和型，比例型，和指数型。

加和型： $P_i= P_{pop} + η_1$

比例型： $P_i= P_{pop} (1+ η_1)$

指数型： $P_i= P_{pop} EXP (η)$

$P_i$为个体参数，$P_{pop}$ 为群体参数
其中,Pi 为个体参数,P∧为群体参数,ηi 为第i个个体的随机效应,ηi 符合均值为0,方差为ω2的正态分布｡
#### 2.残差变异
（１）定义：个体内变异又称为残差变异。为了避免与个体间变异混淆或错误识读，后文中用残差变异一词。残差变异来源于测量误差、实验室间的差异以及模型本身等。其大小反映了预测值相对于观测值的随机变化的程度。残差较大表明同一个受试者在相同剂量和给药间隔内的变异大，模型的预测性不佳。若一个线性动力学药物的残差变异较小，在每个给药间隔内的药动学行为一致，则可准确地预测浓度，并提供理想的治疗方案。

个体内变异：个体预测值相对于实际观测值的偏离，用EPS(ε)表示
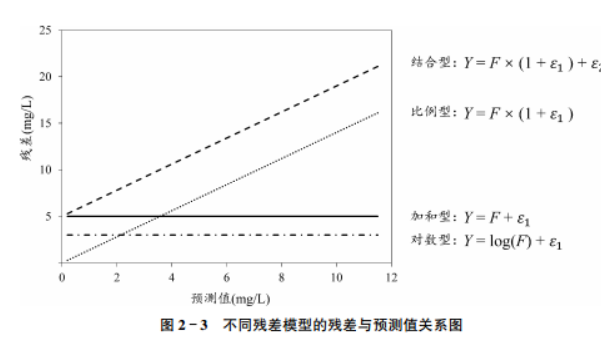
（２）常用函数表达式：加和型，比例型，和指数型。

加和型： $Y = F + ε_1$

比例型： $Y = F（1+ ε_1 ）$

结合型： $Y = F（1+ ε_1 ）+ε_2$

对数型： $Y = log(F)+ ε_1$

$Y$为观测值，$F$ 为预测值ε为残差变异。 残差变异符合均值为０、方差为σ２的正态分布。其中对数型模型假设残差变异为对数正态分布，且Ｆ须为正值。

3.场合间变异

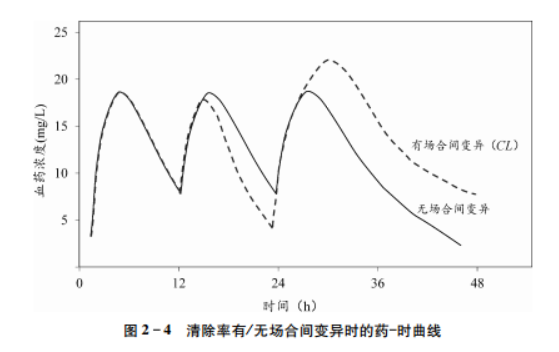
场合间变异（IOV）表示个体的药动学或者药效学参数在不同的研究阶段中的变异，如：不同周期， 不同研究中心
忽略场合间变异可影响个体参数估算值的准确性｡图2 4展示了有无清除率场合间变异时的药时曲线｡

第二节 估算方法

目前,模型参数的估算方法主要有参数法､非参数法和贝叶斯法｡与非参数法相比,参数法的应用更为广泛｡参数法中一阶条件估算法(first order conditionalestimation,FOCE)､含个体间和个体内变异交互作用的一阶条件估算法(first orderconditional estimationwithinter andintrasubject variabilityinteraction,FOCEI)是最经典的计算方法｡贝叶斯法综合了未知参数的先验信息和观测样本信息,根据贝叶斯定理,推断后验信息和未知参数｡

### 一、参数法

常用参数估算方法： 一阶估算法（FO）、FOCE、FOCE-1、拉普拉斯法等

参数法是在假设模型参数服从正态分布(或对数正态分布)的前提下,结合经典的药动学和药效学理论与混合效应模型(固定效应和随机效应),直接求算出群体药动学和药效学参数｡该法是目前群体药动学和药效学研究中使用最为广泛的一种方法｡
1977年,Sheiner教授提出的非线性混合效应模型法(nonlinear mixedeffectsmodeling,NONMEM)采用了参数法估算群体参数｡传统方法一般先计算个体参数,进而计算群体参数｡而非线性混合效应模型法通过统计学模型来处理分析患者的特征信息(病理生理学信息､给药剂量等)､观测值(如血药浓度等)以及可能的误差｡参数估算时,采用了扩展最小二乘法(extendedleast square,ELS法),一步求算所有的群体参数｡
常用的NONMEM软件包提供了多种参数估算方法,包括一阶估算法(first order,FO)､FOCE､FOCEI､拉普拉斯法(Laplace)等｡在NONMEM7以上版本的软件中,还增加了新的算法,包括迭代两步法(iterativetwostagemethod)､蒙特卡洛抽样重要最大期望值法(MonteCarloimportancesamplingexpectationmaximizationmethod)､随机近似最大期望值法(stochasticapproximationexpectationmaximizationmethod)等｡其中FOCE和FOCE I的估算结果准确可靠,是经典的计算方法｡

### 二、非参数法

常用非参数估算方法： 最大似然法（NPML）、非参数最大期望法（NPEM）、半参数法（SNP）

与参数法不同,非参数法无须假设参数符合正态分布(或对数正态分布)即可求算参数,适用于多种概率分布或联合分布的数据｡目前,基于非参数法原理的算法有非参数最大似然法(nonparametricmaximumlikelihood,NPML)､非参数最大期望值法(nonparametricexpectationmaximization,NPEM)､半非参数法(semi nonparametric,SNP)､非参数自适应网格法(nonparametricadaptivegrid,NPAG)等｡Pmetrics软件和NONMEM7. 2以上版本软件纳入了相关算法｡

### 三、贝叶斯法
贝叶斯法由英国学者托马斯·贝叶斯创建｡其基本原理是根据某一事件既往发生的概率特征,预测之后发生该事件发生的可能性｡在群体药动学药效学研究中,贝叶斯法可以根据群体内的参数分布特征和个体实际的观测数据(如血药浓度､生物标志物浓度､药效学效应值等),估算最大概率的个体参数,
最大似然法(maximumlikelihood)估算参数时,假设参数是固定且未知的,但研究数据稀疏､数据不满足正态分布或模型过于复杂时,最大似然法易致计算失败｡与最大似然法不同,贝叶斯法在参数估算时纳入了先验信息,并假设模型参数是随机的｡例如,马尔科夫链蒙特卡洛(MarkovChainMonteCarlo,MCMC)贝叶斯法无须假设参数的分布形式,可从某个建议分布(proposal distribution)中抽取样本,获得稳定的后验分布,进而分析计算｡在稀疏数据建模分析时,MCMC贝叶斯法可作为参数估算的方法｡此外,最大似然法的结果通常是点估算值,如平均值;而贝叶斯法获得的通常是参数的概率分布｡与最大似然法相比,贝叶斯法估算参数基于先验信息,具一定主观性｡当使用不同的先验信息时,可得到不同的估算结果｡因此,贝叶斯法估算的可信度也取决于先验信息的可信度｡尽管如此,贝叶斯法在医学研究中的应用仍日益增加｡2010年,美国FDA颁布了关于应用贝叶斯法分析医疗设备数据的指导原则｡当传统的概率方法失败时,贝叶斯法常常作为替代方法使用｡2011年,NONMEM7.2以上版本软件纳入了MCMC贝叶斯算法｡目前,该方法也成为群体数据分析中的重要算法之一｡