NONMEN 协变量模型
协变量的定义
描述药代动学和药效学的变异来源。协变量模型可 区分群体中可能无法达到药效或产生不良反应的亚群体;明确药动学和药效学行为的影 响因素;提高对药物作用机制的认识和模型的预测能力;也可进一步提出合理假说。
包括:性别、年龄、体重、体表面积、种族、实验室检测指标,疾病状态等
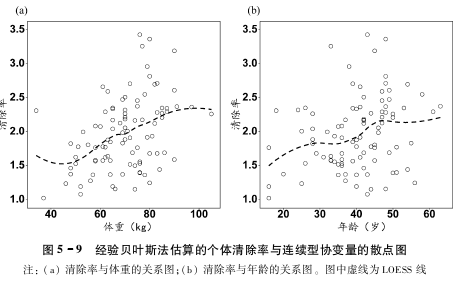
图解法
统计学检验原理
嵌套模型:当考察协变量效应时,所比较的模型须为嵌套模型(nestedmodel)。嵌套模型即模型 结构一致的模型。复杂模型比简单模型的参数更多。但当协变量参数设为0时,复杂模 型可简化为简单模型。例如,一个简单
$$
CL_i=θ_1+θ_2×SEXF_i
$$
$$
CL_i=θ_2+θ_1×WT_i
$$
纳入协变量的模型目标函数下降大于3.84才具有统计学意义
常用函数表达式
一、连续性变量
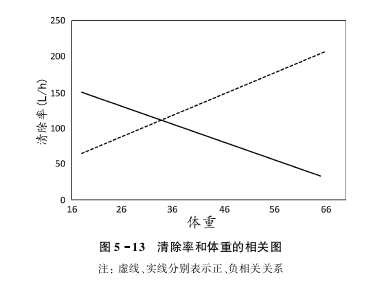
- 线性模型
协变量的取值范围内,药动学或者药效学随着协变量的增大而增加或者减少,则估计的斜率参数($θ_2$)相应地可为正值或者负值。
协变量模型常采用以下形式:
$$CL_i=θ_1+θ_2×WT_i$$
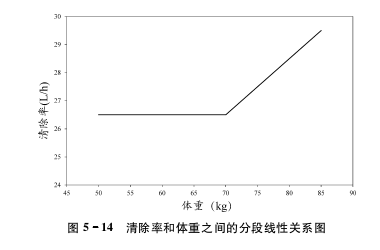
- 分段线性模型
若参数和协变量之间的关系呈现出折线形态,则可采用分段线性模型。如图
参数和协变量之间呈现折线形态如:
$$CL_i=θ_1+θ_2×70×(1-WTind_i)+θ_2×WT_i×WTind_i)$$
- 幂函数模型
幂函数模型可描述参数和协变量之间的多种关系。协变量的幂函 数模型通常采用以下形式:$$CL_i=θ_1×WT_i^{θ_2}$$
-
指数模型
协变量的指数模型通常采用以下形式:$$CL_i=θ_1×e^{θ_2×WT_i}$$
其中,WT_i是第i个个体的体重;θ1为体重为0时的清除率(系数);θ2是估算的指数 (正或负数),反映单位WT变化对应的ln(CL)变化量。
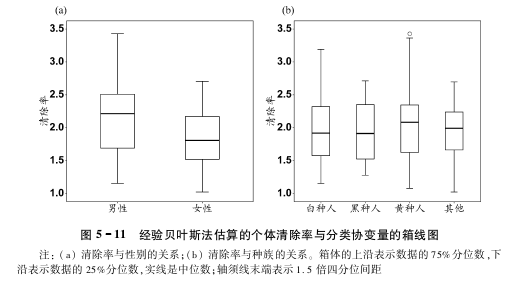
二、分类变量
常用的二分类变量的数学表达式包括加法型和比例型:
加法模型:
$$
CL_i=θ_1+θ_2×SEXF_i
$$
比例模型:
$$
CL_i=θ_1×(1+θ_2×SEXF_i)
$$
其中,指示变量SEXFi取值为0(男性)或1(女性)。θ1为男性药物清除率,θ2为男、 女清除率之间的差值或比例系数,此外,可使用IFTHEN编码语句,如下:
IF (SEXF.EQ.1) THEN
TVCL=THETA(1)
ELSE
TVCL=THETA(2)
ENDIF
CL=TVCL*EXP(ETA(1))
逐步法
协变量模型建立最常使用的方法是逐步法,即分成两步,包括前向纳入和逆向剔除。前向纳入法即采用加法、乘法或指数模型等逐一加入各因素,建立全量模型后,用逆向剔除法考察各影响因素,排除无显著性意义 的固定效应参数后,最后获得最终模型。
一、向前纳入法
向前纳入过程中,将协变量逐个添加至模型中,每次只添加一个,且只在一个参数上进行尝试。假设检验水平α=0.05,若加入某一协变量后,目标函数值的下降超过3.84,则将该协变量加入模型,反之予以剔除。
二、逆向剔除法
向前纳入过程中可能纳入不必要的协变量。导致模型不稳定或者过度参数化。逆向剔除更为严格,如Α=0.001 即目标函数变化大于10.83,则认为该因素有显著意义,模型中予以保留。经过逆向剔除过程,排除无显著性意义的固定效应参数后得最终模型。 协变量的确认还可考虑如下两方面:①参数95
上述逐步回归法可用pSn中的scm命令实现上述过程,自动筛选和考察协变量对模 型参数的影响。此外,一些工具软件也提供了一些自动筛选协变量的手段,如xPOSE中 gam模块,采用了广义加和模型法筛选协变量。
文章评论