PBPK学习笔记：预测代谢酶/转运体介导的药物-药物相互作用

药物相互作用类型

• 动态竞争抑制
• 动态时间依赖- 性抑制
• 动态诱导
  （包括对原型药物和/或代谢产物的影响；包括酶和转运蛋白）

• 稳态竞争抑制

• 稳态时间依赖- 性抑制
• 稳态诱导
  （可能包括施害药物浓度影响代谢产物，不包括转运体）

PBPK 模型

吸收分布代谢过程

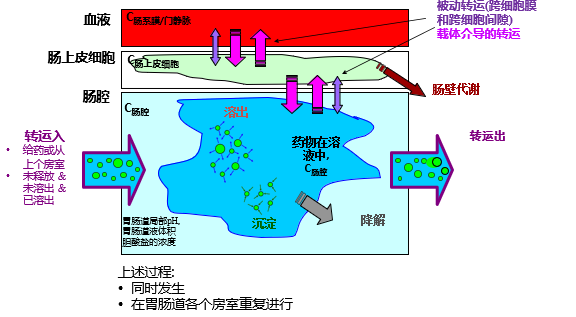
药物在体内转运过程

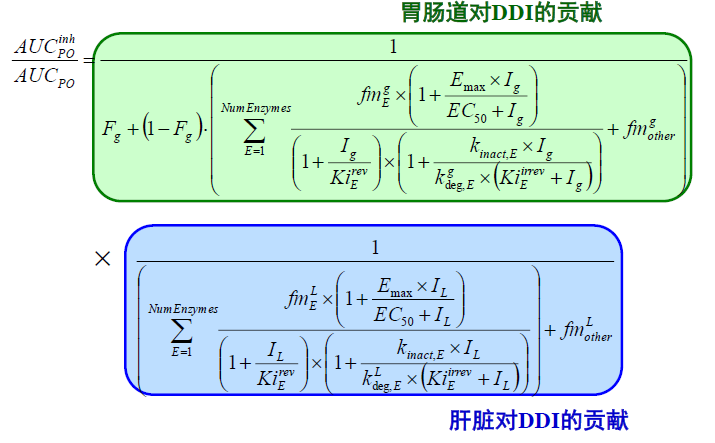
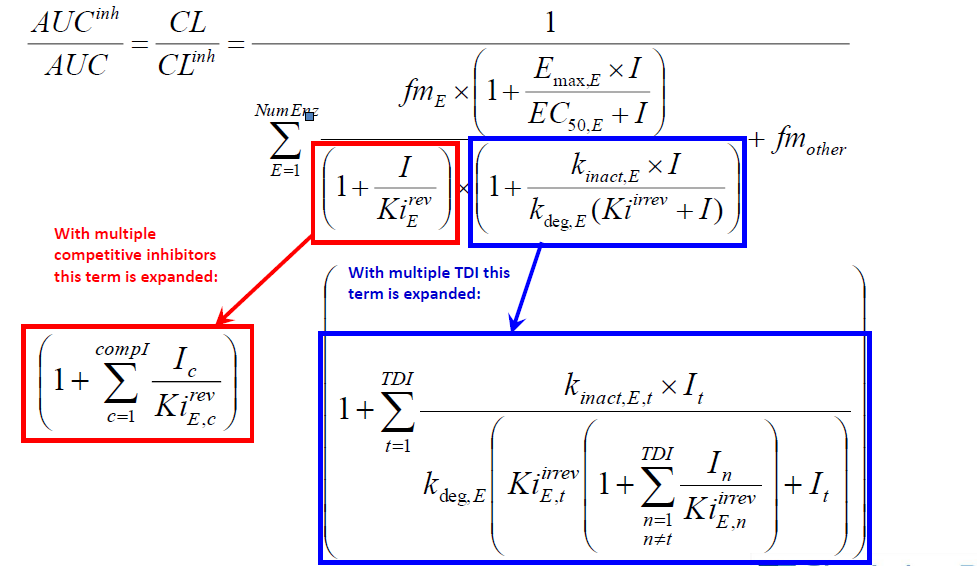
预测稳态DDI- 相关方程

虽然方程中只显示一种抑制剂或诱导剂的影响, 但模拟不同浓度时,母药和代谢物的影响(如它们有影响并且有指定的常数)也会纳入模拟中

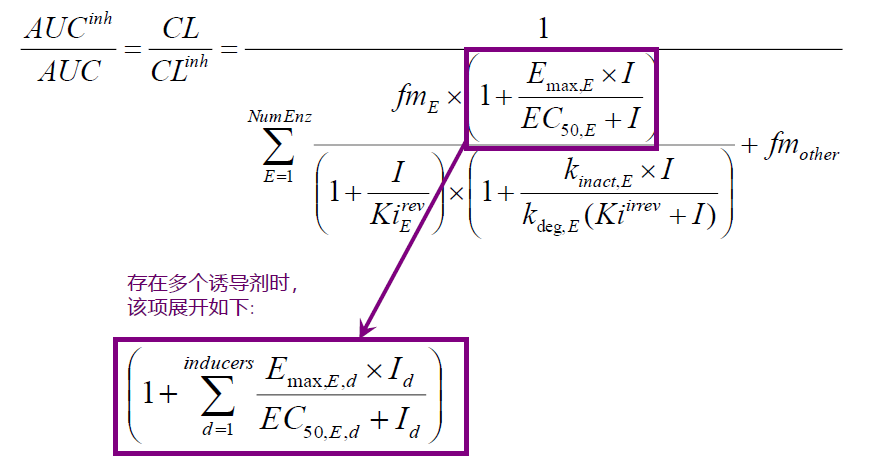
预测稳态DDI– 多个促变药

预测稳态DDI– 多个促变药

预测稳态DDI 时 需要输入的数据

1. 底物（受变药）的 fm 和 Fg 值
2. 抑制剂的Ki (或 IC50)
3. 时间依赖性抑制剂的Kinact [min^-1]
4. 诱导剂的EC50 和 Emax
5. 时间依赖性抑制中酶的转换速率(kdeg [min^-1])
6. 抑制剂或诱导剂（促变药）的浓度:

- 由不同计算方法计算得到，通过抑制剂/诱导剂浓度模拟估算得到
- 抑制剂/诱导剂浓度的模拟，还需整体的PK模型
- 抑制剂/诱导剂浓度的计算，还需输入额外的数据(Fa, FDp, F, ka, kel, etc.)
fm – 某个特定代谢酶占胃肠道酶或总清除率的百分数
Fg – 不被肠道代谢的药物量占总量的百分数，软件中包含了CYPs的默认值kdeg

如何指定药物相互作用的类型

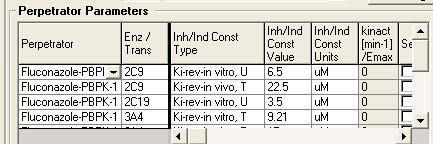
在 Perpetrator Parameters 表中选择 Inhibition/Induction Constant Type.常数类型包括4部分:
1. Ki, IC50 或 EC50 –抑制剂选择Ki 或IC50; 诱导剂选择 EC50
2. rev 或 irr –对于可逆或竞争性抑制剂选择rev; 对于不可逆或时间依赖性抑制剂选择irr(这种选择仅适用于抑制剂且Ki和IC50数据都能获得的情况下)
3. in vitro 或 in vivo – 体外获得的数据(比如微粒体) 或 体内(根据测到的血浆浓度计算得到)
4. U 或 T – 游离型选择U，总量选择T

稳态-促变药的浓度

GastroPlus的DDI模块提供了多种方法来获取促变药的有效浓度，从而可进行稳态DDI的预测
促变药的浓度可通过以下公式计算得到:
1. 体循环平均值:

$$
[I]_{a v}=\frac{D / \tau}{C L / F}
$$

2. 体循环Cmin:

$$
[I]{\min }=[I]{\max } \times e^{-k_e \tau}
$$

3. 肝入口:

$$
[I]{i n}=[I]{a v}+\frac{k_a \times F D p \times D}{Q_h}
$$

4. 肠:

$$
[I]_g=\frac{k_a \times F_a \times D}{Q_e}
$$

D-给药剂量, τ-给药间隔, CL-清除率, kel-消除速率常数, ka-吸收速率常数, Fa-吸收百分数, FDp-通过门静脉的分数,F-生物利用度, Qh-肝脏血流速率, Qe-肠上皮细胞血流速率, Fup[

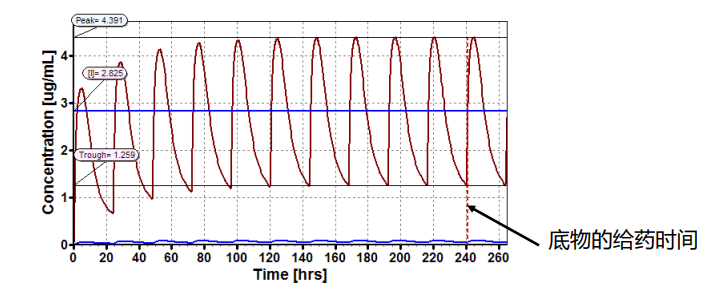
如在底物给药之前，促变药浓度已达到稳态， 促变药在肝脏或血浆中的有效浓度将通过曲线峰浓度与谷浓度的平均值估算得到

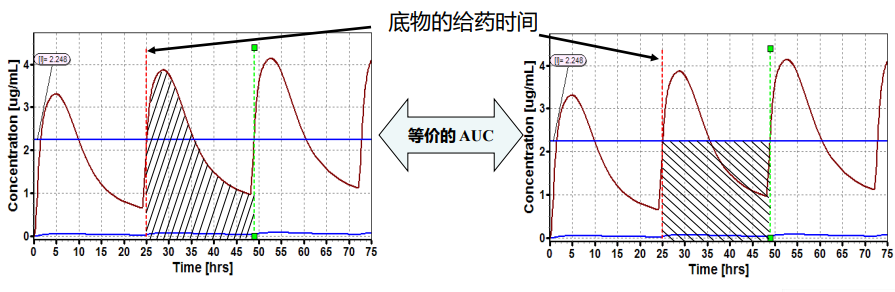
如在底物给药之前，促变药浓度未达到稳态， 促变药在肝脏或血浆中的有效浓度，则通过AUC延伸区间的浓度均值进行估算的，该AUC的选取是在底物给药前的这段间隔区间。

胃肠道中有效的促变药浓度，是通过胃肠道所有房室中肠上皮细胞中浓度的平均值估算得到的； 对各个房室而言, 促变药浓度依据底物给药时间和该房室传输时间，以计算底物在该房室里面停留的时间。

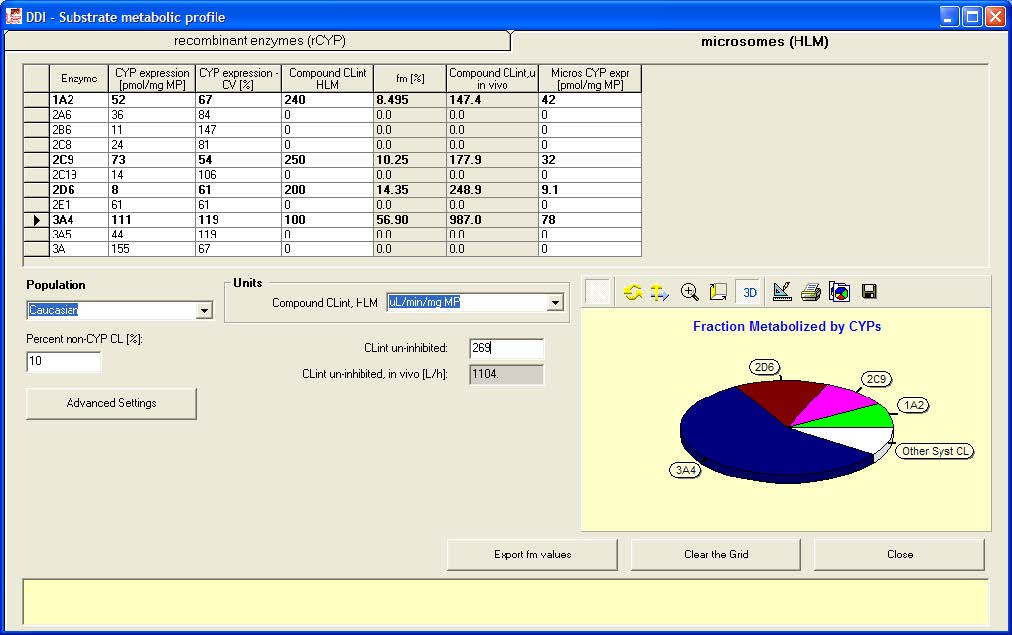
用体外实验估算 fm 值

用户需要输入在重组酶系统及相应的ISEFs中测得的每个酶的体外固有清除数据
如果无法得到ISEFs 数据, 也可以通过输入在 HLM, rCYP 中测得的标准化合物的清除率以及 肝微粒体中每种CYP酶的丰度值直接进行计算:
$ISEF^{r C Y P}=\frac{\langle\text { Standard CLint HLM }\rangle}{\langle\text { Standard CLint rCYP }\rangle \times\langle\text { Micros CYP expr }[\mathrm{pmol} / \mathrm{mg} \mathrm{MP}]\rangle}$

每种酶的体内清除率计算如下:
$\begin{aligned} CL_{\text {int}}^{CYP}= & ISEF^{rCYP} \times\langle\text { Compound CLint rCYP }\rangle \times\langle\text { In Vivo CYP Expr }[\mathrm{pmol} / \mathrm{mg} \mathrm{MP}]\rangle \ \ \times\langle\mathrm{mg} \text { protein } / \mathrm{g} \text { tissue }\rangle \times\langle\text { Tissue Weight }\rangle\end{aligned}$
每种酶的fm值计算如下:
$
f m^{CYP}=\frac{C L_{\text {int }}^{C Y P}}{\sum_{C Y P} C L_{\text {int }}^{C Y P}} \times(100-\langle\text { Percent non - CYP CL }[%]\rangle)
$

操作练习: 预测稳态 DDI

用体外人肝微粒体HLM数据计算fm值
1. 在 File/New Drug Database 菜单栏新建一个database(命名为“Drug1234”)
2. 命名第一个record 为“Drug1234-DDI-HLM”
3. 在Modules (Optional)/8 DDI 菜单栏下打开DDI模块
4. 点击Calculate fm values 按钮以弹出fm 计算 工具
5. 选择表格“microsomes (HLM)”
6. 输入实测的清除率CLint 值269 uL/min/mg MP 并假设有10 7. 输入以下表格中的信息:

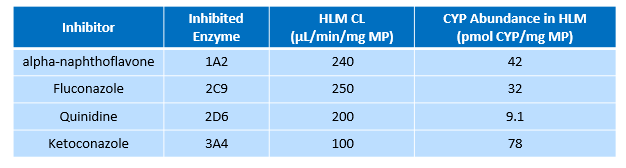
8. 输入结束后, 点击 Export fm values 按钮
9. 预测稳态下与氟康唑的DDI

通过HLM 的体外实验测量值计算底物的

动态DDI的模拟

除了已经包含的药物相互作用PK模型外，动态拟没有做任何假设和简化
1. 需要为受变药和促变药搭建房室或PBPK模型
2. 考虑了任何组织中的药物相互作用
3. 考虑了同一个酶/转运体的多个底物之间的相互竞争以及底物对抑制剂/诱导剂的可能影响
注意: 在同一个系统中针对同一个酶/转运体，多个底物都有特定的km和Vmax，
此时 可以用Ki = Km来表征他们对同一个酶/转运体结合位点的竞争作用
4. 可考察多个不可逆抑制剂对酶结合的竞争作用
5. 可考察一个药物同时做出抑制剂和诱导剂的可能性
6. 所有CYP酶都有默认的生理学参数(表达水平, 转换速率) , 但如用户知道相关的酶/转运体其它数据，应尽可能修改或加入这些参数。

动态DDI的模拟 – 方程

竞争性抑制：

$$
v=\frac{E n z A c t_0 \times V_{\max } \times[S]u}{K_m\left(1+\sum{j=1}^N \frac{[A]{u, j}}{K{m, j}}+\sum_{i=1}^M \frac{[I]{u, i}}{K{i, j}}\right)+[S]_u}
$$

时间依赖性抑制& 诱导

$$
v=\frac{E n z A c t_t \quad \max \times[S]u}{K_m\left(1+\sum{j=1}^N \frac{[A]{u, j}}{K{m, j}}+\sum_{i=1}^M \frac{[I]{u, i}}{K{i, j}}\right)+[S]_u}
$$

$$
\frac{d E n z A c t}{d t}=-\left(\sum_{t=1}^{T D I} \frac{k_{\text {inact,t }} \times[I]{u, t}}{K{i, t}\left(1+\sum_{\substack{n=1 \ n \neq t}}^{T D I} \frac{[I]{u, n}}{K{i, n}}\right)+[I]{u, t}}\right) \times E n z A c t+k{\operatorname{deg}}\left(EnzAct_0-EnzAct\right)
$$

$$
+k_{\mathrm{deg}} \times E n z A c t_0 \times \sum_{d=1}^{\text {inducers }} \frac{E_{\max , d} \times[I]u}{E C{50, d}+[I]_u}
$$

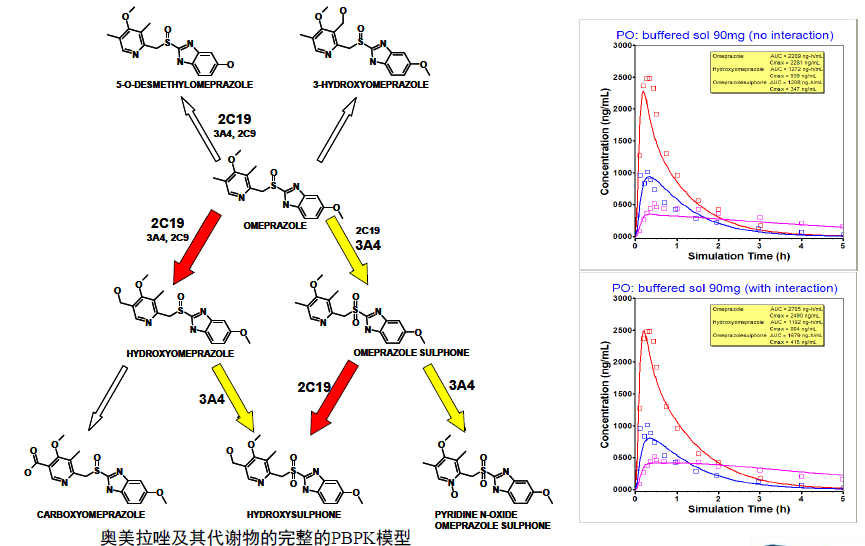
母药和代谢物竞争酶的结合位点

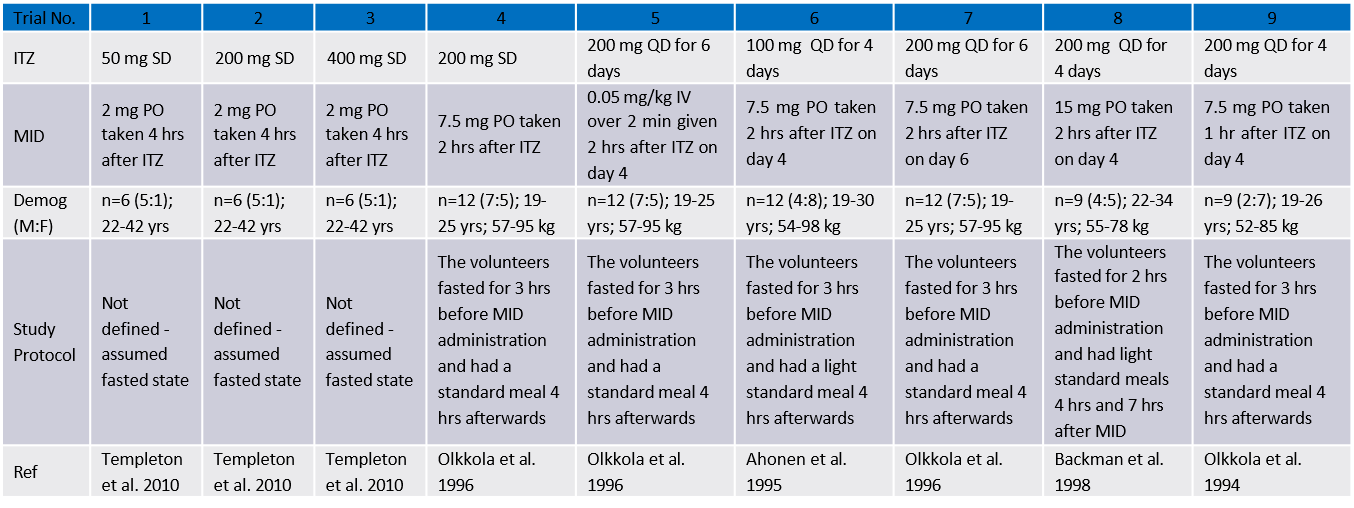
伊曲康唑– 米达唑仑DDI：包括伊曲康唑和3个代谢物的抑制效应

动态 DDI 的模拟 – 需输入的参数

1. 每种抑制剂的Ki (或 IC50)
2. 时间依赖性抑制剂的Kinact [min-1]
3. 每种诱导剂的EC50 和 Emax
4. 时间依赖性抑制/诱导中每种酶/转运体的转换速率kdeg [min-1] (GastroPlus提供 CYPs酶的上述信息)
5. 药物与底物相互作用的完整PK模型
6. (房室或PBPK模型，底物与促变药二者需要相同的模型)
7. 对每一个化合物，只需调整对应的药物相关的性质参数– 其他的生理学参数都是相同的
   注意: 当前 record下（Form的左边）的生理学数据对于相互作用的另一个药物也是可用的

操作练习: 咪达唑仑 DDI 动态模拟

• 采用以下给药方案开展咪达唑仑与酮康唑的DDI预测
• 酮康唑: 每天一次，口服400 mg (午饭后)
• 咪达唑仑: 酮康唑给药的第4天，在酮康唑给药1h后口服7.5mg咪达唑仑

1. 打开Midazolam database，并找到咪达唑仑的一个records ，名称为Human PO Soln 7.5 mg PBPK DDI.
2. 设置胃肠道生理参数Human – Physiological – Fed，并创建一个23岁美国女性的PBPK模型 (体重= 71.63 kg).
3. 这时需改变肝血流量以反映出是餐后状态，在Pharmacokinetics tab窗口下点击“Edit PBPK” 按钮，双击Liver tissue. 设置Blood Flow = 29.7 mL/s (相比空腹状态肝血流量有30
4. 打开DDI模块，并选择动态模拟Dynamic Simulation
5. 酮康唑连续给药4天，每日给药剂量为400mg，第4天在酮康唑给药1小时后，咪达唑仑给药7.5mg
   操作练习的目标:
   A. 平均值的预测: 先进行基线模拟（每个药物与空白安慰剂同服后的情况），并进行全模拟（两个药物同服用后的情况）

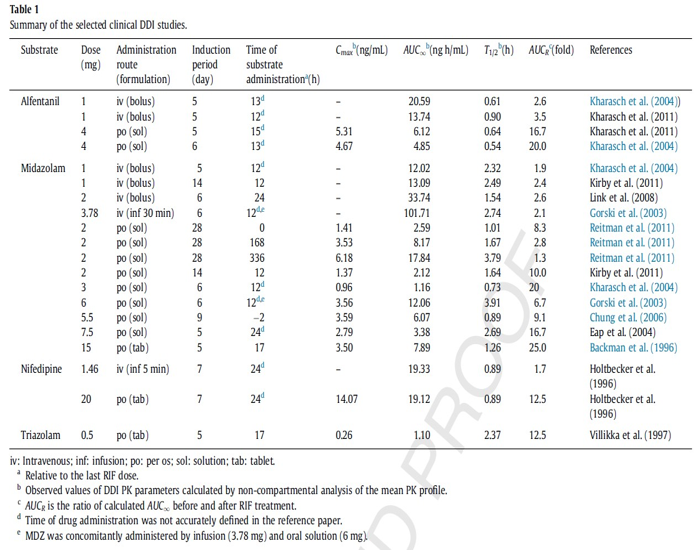
操作练习: 利福平-咪达唑仑诱导DDI

操作练习: 复杂的DDI: 自身诱导, 诱导, 复杂的抑制

1. 打开利福平文件夹下的Rifampicin database，并找到Human – PO – 600 mg record
2. 探索基线模型应该如何设置？
3. 打开 DDI模块，并设置利福平为促变药Perpetrator. 在Rifampicin Data Sheet.xls 中找到抑制/诱导常数值，并输入到模型中。
4. 模拟运行结束后，在DDI模块下的FileOpen Database of Interacting Compounds 菜单打开Rifampicin database 。
5. 选择动态模拟，并设定给药的方案（Rifampicin 每24小时给药600 mg, 给药总时长= 168 hours)
6. 运行DDI预测，并查看结果

操作练习: 复杂的DDI: 自身诱导, 诱导, 复杂的抑制

1. 在FileOpen Database of Interacting Compounds 菜单下，打开Midazolam database

- a)打开database后, 设定Midazolam 为Victim，并选择 Human PO Solution 15 mg record
- b)设定给药方案： 利福平Rifampicin每24小时给药600 mg， 连续给药的第6天，咪达唑仑在利福平给药的1小时后给药15mg。
- c)运行动态DDI模拟，并查看结果。
2. 探索Emax 和Kdeg 的敏感性